A.下界合金II

本来题面上是去掉终点是树来着，但是由于草稿题面上没有写是树，导致最终造的数据不是树。
如果这题是树，可以有可证明时间复杂度的算法。
不过鉴于dfs剪枝也能通过本题，本题不再修正。
由于只有很少的结点，搜索即可。由于pg永远不会回头，注意打标记。

#include<bits/stdc++.h>
using namespace std;

vector<int>e[110];
int a[110];
bool vis[110];
int n,m,k;

bool reachable(int x,int now)
{
    if(x==n) return true;
    if(vis[x]) return false;
    if(a[x]<0) now+=-a[x];
    else now-=a[x];
    if(now<0) return false;
    vis[x]=true;
    for(int i=0;i<int(e[x].size());i++)
    {
        if(reachable(e[x][i],now)) return true;
    }
    vis[x]=false;
    return false;
}

int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++)
    {
        int u,v;
        cin>>u>>v;
        e[u].emplace_back(v);
        e[v].emplace_back(u);
    }
    if(reachable(1,k)) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}

B.收集神瞳

根据题意模拟即可，比较一下传送后走过去的距离和直接走过去的距离，选择最优累加。

#include <stdio.h>
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n, q;
    double a, b, x1, y1, sum=0.0, x[505], y[505];
    cin>>n>>q;
    for(int i=0;i<n;i++)
    {
        scanf("%lf%lf",&x[i], &y[i]);
    }
    x1=x[0],y1=y[0];
    while(q--)
    {
        scanf("%lf%lf",&a,&b);
        double d=(a-x1)*(a-x1)+(b-y1)*(b-y1);
        for(int i=0;i<n;i++)
        {
            d=min(d,(a-x[i])*(a-x[i])+(b-y[i])*(b-y[i]));
        }
        sum=sum+sqrt(d);
        x1=a, y1=b;
    }
    printf("%f",sum);
    return 0;
}

C.No A+B!

签到题，根据题意输出即可通过。

D.赌场豪劫

签到题，根据题意输出即可，注意if和else的使用。

E.单词记忆

贪心基础题。
举个例子，对于单词1 1 2 2 2 2 2 2 3 3 3 3 3，我们排序后遍历整个数组。
首先天数为1的只能放在第一天，这一点毋庸置疑，这时结果如下：
1 2
然后我们开始放天数为2的单词，当放到这里的时候
1 2
3 4
我们发现，我们可以将剩下的天数为2的单词放到第一天
1 2 5
3 4
天数为2的单词可以放在第一天或第二天，然后我们接着放2
1 2 5 7
3 4 6 8
天数为3的单词以此类推，当第三天被放满之后，我们就开始考虑放到前面。或者当前面的天数有空位的时候，我们直接去填充空位。

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <deque>
#include <iostream>
#include <map>
#include <deque>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#include <bitset>
#define pi acos(-1)
#define hu(x) x*pi/180.0
using namespace std;
typedef long long ll;
ll lceil(ll a,ll b){
    if(a%b==0) return a/b;
    return a/b+1;
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int n,m;
    cin>>m>>n;
    pair<int,int> num[n];
    for (int i = 0; i < n; ++i) {
        cin>>num[i].first;
        num[i].second=i+1;
    }
    sort(num,num+n);
    int re=lceil(n,m);
    int day=1;
    int j=0;
    // bool f=0;
    int i;
    for (i = 0; i < n; ++i) {
        if(num[i].first==1) re=max(re,i+1);
        else {

            break;
        }
    }
    //out<<i<<" "<<re<<endl;
    if(i!=0) day++;
    if(i!=0&&i<re) i=re;
    for ( ; i < n; ++i) {
        j++;
        if(j>=re&&i+1==n){

            if(j>re) re++;
            break;
        }
        if(j==re&&num[i+1].first>day){
            day++;
            j=0;
        }
        else if(j>re){
            re++;
            i+=day-1;
            j--;
        }
    }
    cout<<re<<endl;
    int c=0,k=0;
    for (int i = 0; i < re*m; ++i) {
        if(k==n) cout<<0<<" ";
        else {
            cout<<num[k].second<<" ";
            k++;
        }
        c++;
        if(c==re){
            cout<<endl;
            c=0;
        }
    }
    return 0;
}

F.14.7

向八个方向查找，只要任意一个方向能找到就输出YES，否则输出NO。

#include <bits/stdc++.h>
using namespace std;
#define inf 0x7fffffffffff
#define N 500500
#define mod 1000000007
#define mod2 998244353
#define ok printf("ok\n");
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define der(a) printf("der=%lld\n",a);
#define ll long long
double a[110][110];//看题面的数据范围
int dx[8]= {0,0,-1,1,1,1,-1,-1};
int dy[8]= {1,-1,0,0,1,-1,1,-1};//八个方向
int main()
{
    ll n,m,x,y;
    //ll 是上面定义的宏 为long long
    scanf("%lld%lld%lld%lld",&n,&m,&x,&y);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%lf",&a[i][j]);//输入矩阵
        }
    }
    bool bl=0;//标记：能否跨出14.7
    for(int i=0;i<8;i++)
    {//遍历八个方向
     //尝试每个方向走到最后
        double sum=0;
        ll xx=x;
        ll yy=y;//初始化
        while(1)//直跨到底
        {
            if(xx<=0||xx>n||yy<=0||yy>m)//判定边界
            {
                break;
            }
            sum+=a[xx][yy];//统计跨越的距离
            xx+=dx[i];
            yy+=dy[i];//往现在的方向走一步
        }
        if(fabs(sum-14.7)<0.000001)//判断是否满足条件(PS:不能用“==”来判断，因为是浮点数的底层原因，详细情况请查百度)
        {
            bl=1;//满足条件
            break;
        }
    }
    //输出答案
    if(bl==1)
    {
        printf("YES\n");
    }
    else
    {
        printf("NO\n");
    }
    return 0;
}

G.从南到北

在每一组中遍历一遍，找最大值，用一个变量加起来输出。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define imax 0x3f3f3f3f
#define lmax 0x3f3f3f3f3f3f3f3f


int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    int re=0;
    for(int i=0;i<n-1;i++){
        int k,s;
        cin>>k;
        int mx=0;
        for(int j=0;j<k;j++){
            cin>>s;
            mx=max(s,mx);
        }
        re+=mx;
    }
    cout<<re<<endl;
    return 0;
}

H.瑄与洛的约定

结论1：走k步后能到达的位置的横纵坐标之和与k奇偶性相同
结论2：k与$x\ +\ y$奇偶性相同且$k\geq\ x\ +\ y\ $时一定可以恰好k步到达

解释1：k为奇数时有两种情况：①：在x方向上移动奇数步，在y方向上移动偶数步
②：在x方向上移动偶数步，在y方向上移动奇数步
由于每次必须移动不能停在原地，①情况最终横坐标为奇、纵坐标为偶；②情况最终横坐标为偶、纵坐标为奇。两种情况$x\ +\ y\ $均为奇数。
k为偶数时证明方法同上。

解释2：k与x\ +\ y奇偶性相同且$k\geq\ x\ +\ y\ $时的一种合理走法是先花费$x\ +\ y$步从起点走到$(x,\ y)$，此时还需走$ k\ – (x + y)$步，由$k 与 x\ +\ y$ 奇偶性相同可知$k\ – (x + y) $为偶数，此时可以在$(x,\ y)$处重复$(k\ – (x + y)) / 2 $次 向右走->向左走 操作即可。

//木の葉舞う所に，火は燃ゆる。
#include <iostream>
#include <sstream>
#include <cstdio>
#include <cstdlib>
#include <iomanip>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <deque>
#include <stack>
#include <string>
#include <cstring>
#include <vector>
#include <cmath>
#include <bitset>
#include <ext/rope>
#include <unordered_set>
#include <unordered_map>
#define int long long
using namespace __gnu_cxx;
using namespace std;
typedef long long ll;
const int N = 1e3 + 10, M = 510;
const double eps = 1e-5;

void solve()
{
    int x, y, k; cin>>x>>y>>k;
    cout<<((x + y) % 2 == k % 2 && k >= x + y ? "YES" : "NO")<<endl;
}

signed main()
{
    ios;
    int t = 1; cin>>t;
    while(t --) solve();
    return 0;
}

I.星星点灯

签到题，排序后统计k个最大值的和即可，

J.瑄的披萨店

结论1：$\left|x-a\right|+\left|x-b\right|\geq|a-b|$, 当且仅当x在 $[min(a,b),max(a,b)]$ 区间上时取得最小值。
结论2：披萨店选在非降序排序的第 $\frac{n}{2}+1 $个需要配送的位置一定为一个最佳答案。
解释1：在数轴上画出任意两点a、b，则 $\left|x-a\right|+\left|x-b\right| $代表的实际意义为x到a、b两点的距离之和，画出图即可验证当x当且仅当位于 两点之间 或 两点上 时可取得最小值$|a-b|$。
解释2：将所有需要配送的n个位置按非降序排序，假设披萨店放的位置在数轴x位置上：披萨店到所有配送点的和 ${Sum=\ |a}_ 1- x |+\left|a_2-x\right|+\ .. \ + |a_n-x|$
当n为奇数时：

$$ {Sum=\ |a}_ 1-x|+ \left|a_n-x\right|+\left|a_2-x\right|+\left|a_{n-1}-x\right|+\ldots\ +\left|a_{\frac{n}{2}+1}-x\right|$$

$$ \ \geq\left|a_1-\ a_n\right|+\left|a_2-\ a_{n-1}\right|+\ldots+\ |a_{\frac{n}{2}+1}-x|$$

此时除了最后一项都是定值，x 取 $a_{\frac{n}{2}+1} $时最后一项取最小值0且其他项也取得最小值（此时x 在 每项的最小值区间上，$\left[a_1,\ a_n\right],\ \ \left[a_2,\ a_{n-1}\right]\ldots$）。
当n为偶数时：

$${Sum=\ |a}_ 1-x| + \left|a_n-x\right|+\left|a_2-x\right|+\left|a_{n-1}-x\right|+\ldots\ +\left|a_\frac{n}{2}-x\right|+\ \left|a_{\frac{n}{2}+1}-x\right|$$

$$\geq\left|a_1-\ a_n\right|+\left|a_2-\ a_{n-1}\right|+\ldots+\ |a_\frac{n}{2}-a_{\frac{n}{2}+1}|$$

此时均是定值，x 取 $a_\frac{n}{2} $或$ a_{\frac{n}{2}+1}$ 时其他项均取得最小值。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main()
{
    ll n, a[100005], l=0, r=0, ans;
    scanf("%lld",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%lld",&a[i]);
    }
    sort(a,a+n);
    int x=a[(n-1)/2];
    for(int i=0;i<=(n-1)/2;i++)l+=a[i];
    for(int i=(n-1)/2+1;i<n;i++)r+=a[i];
    if(n&1)ans=r-l+x;
    else ans=r-l;
    printf("%lld",ans);
    return 0;
}

K.转折点

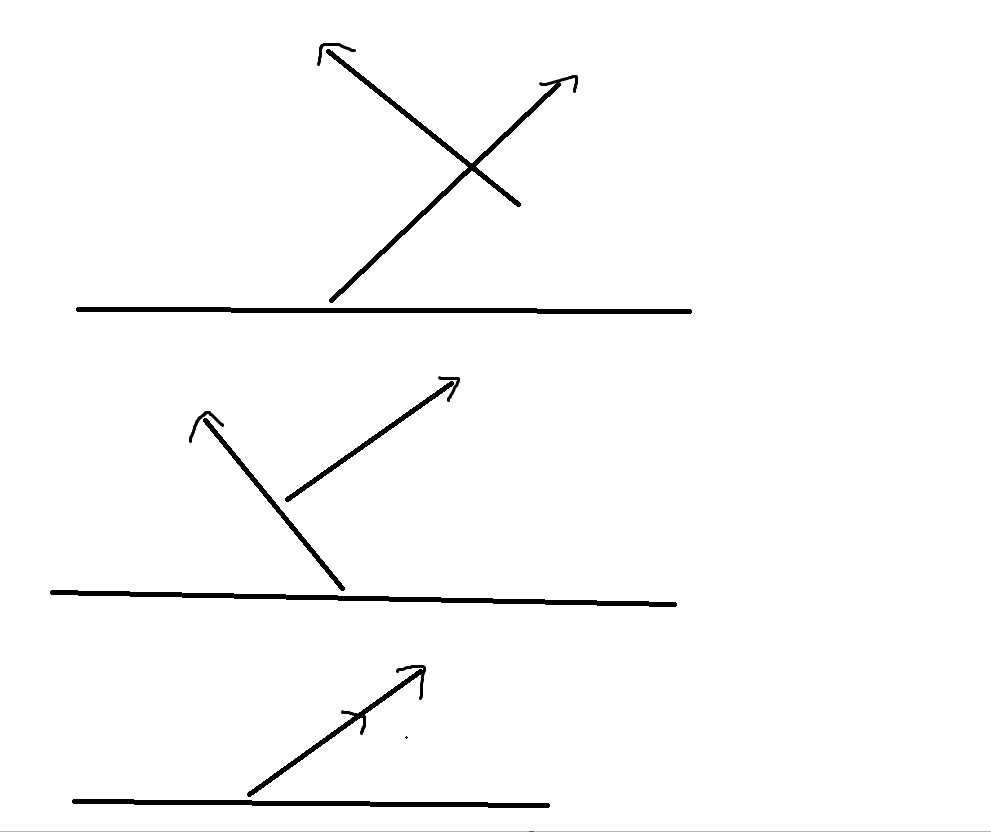
本场比赛的压轴题，基础计算几何。

如图所示，第一种情况为相交，如果相遇时间小于1s，可能会射中。
第二种情况为相离，如果箭的速度足够快，也能在1s内擦过。
第三种情况为重合，直接比较速度即可判断。
其他情况一律为NO。
如果用直角坐标方程，当直线垂直x轴时需要特殊处理。

#include<bits/stdc++.h>
using namespace std;

const double pi = acos(-1);
const double eps = 1e-8;

inline double torad(double x)
{
    return x * pi / 180;
}

inline bool dequals(double x, double y)
{
    return fabs(x - y) < eps;
}

inline bool tequals(double x, double y)
{
    return fabs(x - y) < 1;
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        double theta, alpha, xm;
        cin >> theta >> alpha >> xm;
        double va, vb;
        cin >> va >> vb;
        double x0, y0;
        cin >> x0 >> y0;
        theta = torad(theta);
        alpha = torad(alpha);
        if (dequals(theta, alpha))
        {
            if (dequals(x0, xm))
            {
                if (dequals(theta, pi / 2))
                {
                    if (va > vb) cout << "YES" << endl;
                    else cout << "NO" << endl;
                }
                else cout << "NO" << endl;
            }
            else if (dequals(y0 / (x0 - xm), tan(theta)))
            {
                if (va > vb) cout << "YES" << endl;
                else cout << "NO" << endl;
            }
            else cout << "NO" << endl;
        }
        else if (dequals(theta, pi / 2))
        {
            double x1 = xm;
            double k = tan(alpha);
            double b = y0 - k * x0;
            double y1 = k * x1 + b;
            if (alpha<pi / 2 && x1<x0 || alpha>pi / 2 && x1>x0) cout << "NO" << endl;
            else if (tequals(sqrt(pow(x0 - x1, 2) + pow(y0 - y1, 2)) / vb, y1 / va)) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
        else if (dequals(alpha, pi / 2))
        {
            double x1 = x0;
            double k = tan(theta);
            double b = -xm * k;
            double y1 = k * x1 + b;
            if (y1 < y0) cout << "NO" << endl;
            else if (tequals(sqrt(pow(x1 - xm, 2) + pow(y1, 2)) / va, (y1 - y0) / vb)) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
        else
        {
            double ka = tan(theta);
            double ba = -xm * ka;
            double kb = tan(alpha);
            double bb = y0 - x0 * kb;
            double x1 = (bb - ba) / (ka - kb);
            double y1 = ka * x1 + ba;
            if (alpha<pi / 2 && x1<x0 || alpha>pi / 2 && x1>x0) cout << "NO" << endl;
            else if (tequals(sqrt(pow(x0 - x1, 2) + pow(y0 - y1, 2)) / vb, sqrt(pow(xm - x1, 2) + pow(y1, 2)) / va)) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
    }
    return 0;
}